Let's continue 3d VI - ray intersection

graphic illustrating the ray intersection: A plain square swayed into space a bit is crossed by a line connecting a point before and another point behind that plane. We need the program to render edges intersecting the projection plane.

Here, in the first image, you see an edge that goes right through the screen.

The edge is defined by two Points, one before and one behind the screen plane.

For the mathematical task of calculating the intersection of edges with the screen plane (or any plane at all), we use the concept of "rays"

A ray is always infinite

In the image, you can see two Points in 3d-space connected by a line.

But remember: A ray is specfied as a directed line in the 3d-space with infinite length, though - not limited by one of the points.

Any 3d-ray can be represented mathematically as 2 3d-vectors: One specifying a start location in 3d space and the other specifying the direction of the ray from that point.

Any Point p ∈ Ray is composed of V_Location + x * V_Direction

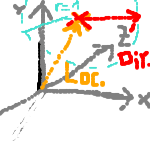
basic vector representation: An example Location and Direction Vector - the latter with length 1 - are connected to build what we call a vector.

Here the example of a basic vector representation: The direction vector is normalized and thus always points onto the edge of a sphere of radius 1 around the point that the Location part of the ray specifies.

Now we try to calculate where the ray intersects a specific plane, for example z=0 or z=1

The base planes z=0 and z=1 are the two relevant planes for most simple z-Projection. Why? z=0 because it's the most intuitive. And z=1 for any projection after we have constated that a division "by (z+1)" instead of "by z" must be done in order to perform a projection - which lets us respect that a point on the z-plane (like (1,0,0), (0,1,0) could not be projected before since a division by 0 occured!

There are three cases:

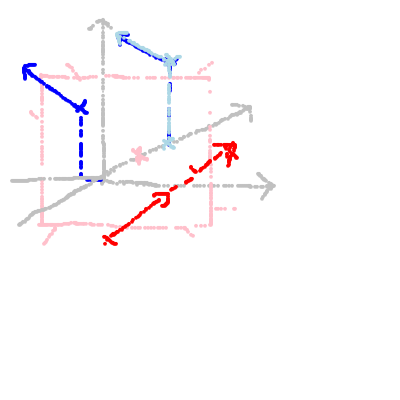
Graphical Illustration of the 3 cases with a pink screen plane defined by z=1. Case 1 is blue, Case 2 lightblue. Case 3 is red.

Case 1: The ray is on the plane - the z-Component of the Rays Location Vector is 0 (or 1), and the z-Component of the Direction Vector is 0 (or 1), too.
Case 2: The ray is parallel to the plane - the z-Component of the Rays Location Vector is NOT 0 (or 1), and the z-Component of the Direction vector is 0 (or 1)
Third Case: The ray intersects the plane: The z-Component of the Direction vector is NOT 0 (or 1, respectively.)

Continue here: Let's Continue 3d VII - Trying to set up a 3d context

Or jump directly to VIII: Ray Intersection Continued