Simple 3d

Every point of a thought plane, edge or point (thought in 3-dimensional space) gets projected onto the screen

For the first realisation of simple projections, we resign on using a camera location (read more about that later on, on the page after the next) and choose the frame of projection to be spanned up by the four points (-1,1,0), (1,1,0), (1,-1,0) and (-1,-1,0) - marked orange in the following graphic:

Also, i drew in a Point called P at the location (1,1,1) that we're going to project to the orange plane now.

The formula for doing that is basic and simple: The X and Y coordinates get just divided by the Z coordinate each:

X_screen = X_{3d coordinate system} / Z_{3d coordinate system} and
Y_screen = Y_{3d coordinate system} / Z_{3d coordinate system}

so that any points that are more in the distance (higher Z) get transformed to points that are closer to the mid of the screen (the result of the projection) - the 2d origin (0, 0).

For example, you have the point (1,1,1) Projected to (1,1) like this.
But the point (1,1,100) gets transformed to (1/100, 1/100) = (0.01, 0.01)

The next graphic shows that a little bit more clearer, maybe:

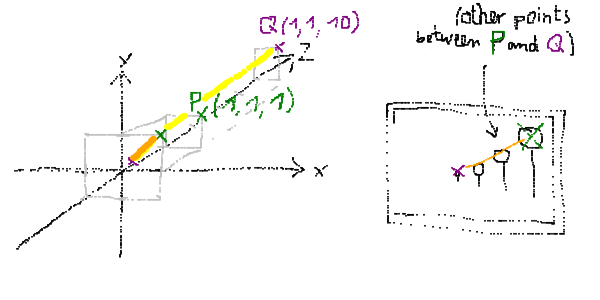
I entered the two points P(1,1,1) and Q(1,1,10) into the projection system.
The yellow line highlights their direct connection in 3d-space. The orange line is the same line projected onto the screen. There (on the screen) you find projected P and Q highlighted with green and purple X-es. On the right, i showed how a real painter would interpret the situation, adding in two additional points in between P and Q, drawing all points as pins connected to the earth or lets say trees.

Outlook

 

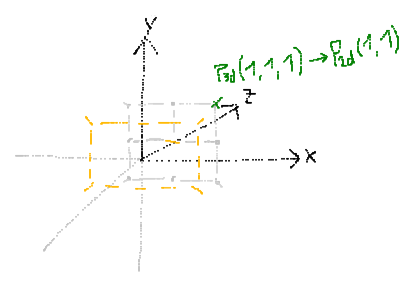
Now, if you are mathematically aware, you might have noticed that actually, doing so, the points all become projected to a plane spanned up by the four points (-1,1,1), (1,1,1), (1,-1,1) and (-1,-1,1) instead of (-1,1,0), (1,1,0), (1,-1,0) and (-1,-1, 0) (that means, the frame residing on plane z=1 instead of plane z=0):

And also note that you must be aware of not dividing through zero. Read more about that (and what we do about it) on the next page: Let's continue 3d III